import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import ConnectionPatch
from PIL import Image
import plotly.io
import plotly.graph_objects as go
# colab: coloab
# jupyter lab: jupyterlab
# jupyter notebook, quarto blog: notebook
plotly.io.renderers.default = "notebook"친절한 디퓨전 모델 1편: DDPM 이론편
2022년 8월 스테이블 디퓨전이 발표되고 약 1년이 지난 지금 스테이블 디퓨전 모델을 실행하는 툴 사용법에 대한 동영상이 유튜브에 넘쳐나고, 해당 툴로 만들어진 수많은 이미지들이 civitai 같은 사이트에 모델과 함께 개시되고 있습니다. AI 기술이 실 생활에도 영향을 미칠 정도로 발전했다는 것을 보여주는 사례이며 2022년에 발표된 스테이블 디퓨전이 이런 현상을 주도했습니다.
2023년 현재 인공지능 학습은 파인튜닝을 중심으로 재편되고 있는것 같습니다. 이전에는 인공지능 알고리즘의 원리를 정확히 파악하고 이를 구현하는 것이 목적이었다면 이제는 모델을 자기 목적에 맞게 파인튜닝할 수 있는것이 더 중요한 목표가 되었습니다. 앞서 이야기한 많은 디퓨전 관련 컨텐츠들도 모두 파인튜닝을 이용한 것들입니다. 파인튜닝을 잘하기 위해서 어느 정도 모델의 원리를 이해할 필요가 있습니다. 하지만 처음부터 모델을 구현할 정도로 원리를 깊게 이해할 필요는 없습니다. 이런 생각에는 여러 이견이 있을 수 있지만 학습의 트랜드가 파인튜닝을 중심으로 변하고 있다는 사실 자체를 부인할 수는 없을 것 같습니다.
트랜드를 따라가는 것도 중요한 일이지만 조금 뒤처져서 여유있게 이전과 마찬가지로 모델의 원리를 납득할 만한 수준, 다시말해 원리를 이해하고 이해한 원리가 맞는지 코드로 실행해서 확인하는 수준으로 파악하는 것이 여전히 즐거운 분들이 계실것입니다. 이 블로그에 있는 모든 글은 그런 분들을 위해 쓰여진 글들이므로 이번에도 디퓨전 모델에 대해 그 수준으로 알아보는 글을 게시하게 되었습니다.
이 글은 디퓨전 모델을 잘 이해하기 위해서 스테이블 디퓨전의 근간을 이루는 Denoising Diffusion Probabilistic Models[1] 논문을 리뷰합니다. 쉽지 않은 과정이지만 예전처럼 최대한 건너뜀 없이 친절하고 자세히 알아보도록 하겠습니다.*
* 이 글은 고등학교 수준의 확률 지식과 약간의 다변수 함수에 대한 지식을 가진 공과대학 4학년 또는 석사 1, 2학기 수준에 맞춰져 있습니다.
이 글은 다음 링크를 통해 구글 코랩에서 직접 실행하며 읽을 수 있습니다.
리버스 프로세스
아래 그림은 Denoising Diffusion Probabilistic Models 논문(줄여서 DDPM)을 대표하는 그림입니다. 그림에서 \(\mathbf{x}_0\)는 노이즈 없는 깨끗한 이미지 데이터를 의미합니다. 학습을 위해 모은 데이터 셋에서 샘플 하나입니다. 그림은 이 이미지 \(\mathbf{x}_0\)에 단계적으로 노이즈가 확산되는 과정을 오른쪽에서 왼쪽으로 나타내고 있고 반대로 왼쪽에서 오른쪽으로 노이즈가 제거되는 과정을 나타내고 있습니다.
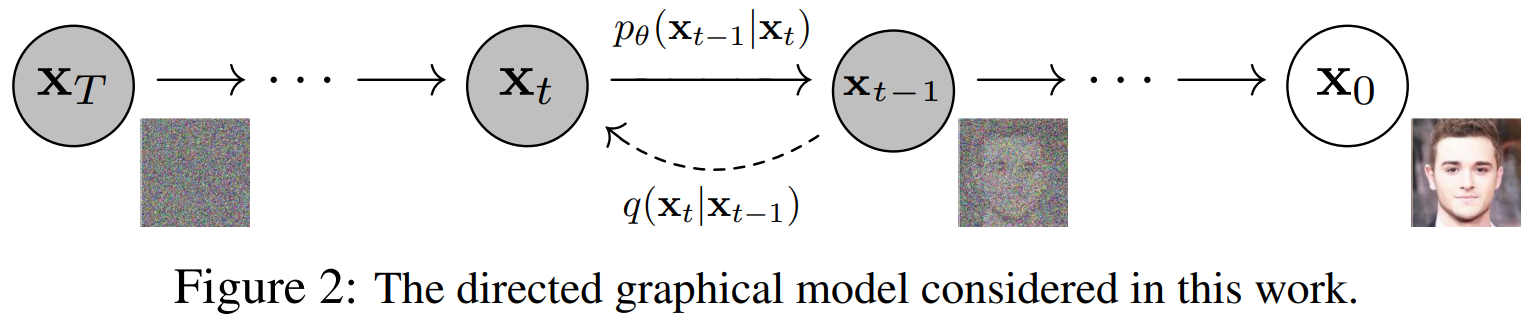
이미지 \(\mathbf{x}_0\)는 숫자 여러 개로 이뤄진 벡터 데이터입니다. 이미지의 픽셀이 숫자 하나에 해당합니다(컬러 이미지라면 픽셀당 숫자 세개). 개별 숫자가 어떤 값을 가지느냐에 따라 우리 눈에 보이는 모습이 달라지게 됩니다. 각 픽셀의 값이 특정 확률 분포를 따른다고 보면 \(\mathbf{x}_0\)는 개별 숫자가 확률 변수인 다차원 확률 변수라 할 수 있습니다. 깨끗한 이미지 \(\mathbf{x}_0\)가 확률 변수라면 이 변수가 따르는 분포가 있을 것이고 이를 다음처럼 표시할 수 있습니다.
\[ \mathbf{x}_0 \sim q(\mathbf{x}_0) \]
분포 \(q\)는 이미지 공간에 원래 존재하는 분포입니다. 하지만 이 분포가 어떤 것인지 알지 못합니다. 만약 \(q(\mathbf{x}_0)\)를 정확히 알고 있다면 이 분포에서 샘플링을 하기만하면 데이터 셋과 동일한 종류의 깨끗한 이미지를 다양하게 얻을 수 있을 것입니다. DDPM 논문에서 \(q\)라고 적는 분포는 원래 존재하는 분포, 다시말해 알아내고 싶은 분포를 의미합니다.
이미지가 확률변수고 이 확률변수가 따르는 분포로 부터 샘플링해서 또 다른 이미지를 만들어 낸다는 이야기가 너무 이상하게 들릴 수 있습니다. 구체적인 이해를 위해 실험을 해보겠습니다.
다음 셀을 실행해서 16x16x3 크기를 가지는 스프라이트 이미지 데이터 셋을 다운 받습니다. 해당 데이터 셋은 deeplearning.ai에서 제공하는 숏코스 How Diffusion Models Work에서 사용하는 데이터 셋입니다.
!gdown 1gADYmo2UXlr24dUUNaqyPF2LZXk1HhrJDownloading...
From: https://drive.google.com/uc?id=1gADYmo2UXlr24dUUNaqyPF2LZXk1HhrJ
To: /home/metamath/etc/repo/blog/posts/diffusion/sprites_1788_16x16.npy
100%|██████████████████████████████████████| 68.7M/68.7M [00:06<00:00, 10.8MB/s]다운 받은 데이터 파일을 로딩하고 255로 나눠 픽셀값을 0~1사이로 노멀라이즈 합니다.
sprites = np.load('sprites_1788_16x16.npy')# 준비된 (64,64)크기의 나비 이미지를 (28,28)로 리사이즈하고
# 픽셀값을 0~1로 노멀라이즈
x0 = (sprites / 255)[10]
# 노멀라이즈 확인
print(x0.min(), x0.max())0.0 1.0다운받은 이미지를 화면에 출력해봅니다.
plt.imshow(x0)
plt.show()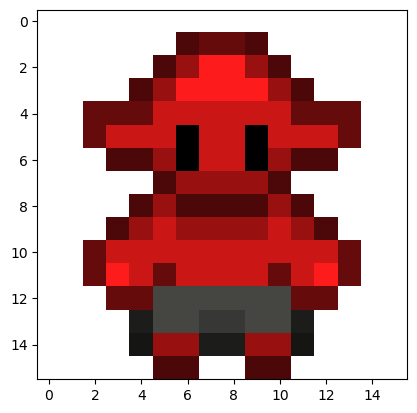
이제 x0가 확률변수라는 것을 실험해보기 위해 scipy에서 제공하는 다변수 정규분포 multivariate_normal를 임포트 합니다.
# x0가 확률변수라는 것을 실험해보기 위해 다변수 정규분포를 임포트
from scipy.stats import multivariate_normalx0를 16x16x3=768개 숫자를 가지는 벡터 변수로 보고 방금 준비한 x0을 평균으로 하는 정규분포 q_x0를 생성합니다.
# 이미지를 768차원 확률 벡터 변수로 만들고
x0_flt = x0.reshape(-1)
# 이 이미지 x0_flt를 평균으로 하고
# 0.1정도되는 적당한 수를 곱해서 공분산을 만들어 정규분포를 정의
# 이 수가 커지면 평균으로 부터 멀리 떨어진 이미지까지 샘플링되고
# 작으면 평균과 거의 비슷한 이미지들만 샘플링됨
q_x0 = multivariate_normal(mean=x0_flt, cov=0.1 * np.eye(len(x0_flt)))생성된 분포 q_x0에서 값 3개를 샘플링해서 화면이 그려봅니다.
# 3개만 샘플링 해서
samples = q_x0.rvs(size=3)
# 크기를 보면 (3,768)
print(samples.shape)(3, 768)768차원 벡터 변수 3개가 샘플링 되었고 이를 적당히 모양 조정해서 화면에 그리면 다음처럼 그려집니다.
# x0 주변에서 임의로 선택된 샘플들
plt.imshow(samples.reshape(3,16,16,3).transpose(1,0,2,3).reshape(16,-1,3).clip(0,1))
plt.show()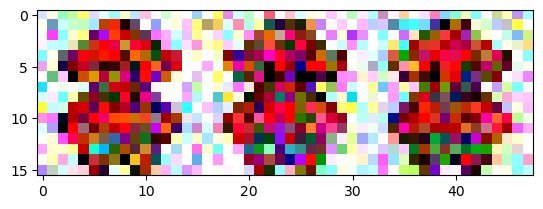
나타나는 그림은 샘플링을 시도할 때마다 조금씩 달라지게 되고 q_x0를 만들 때 설정한 분산 cov에 곱하는 숫자 0.1을 더 크게 할 수록 점점 더 노이즈가 많은 이미지가 샘플링 될 수 있습니다. x0 주변에서 완전히 엉뚱한 노이즈 이미지가 샘플링되는 것이 아니라 평균 이미지를 중심으로 노이즈가 낀 이미지가 샘플링되는 것은 분명히 확인할 수 있습니다.
이미지를 나타내는 변수 \(\mathbf{x}_0\)가 확률변수라는 점을 실험을 통해 분명히 했으므로 나머지 내용을 계속 이어가도록 합시다.
DDPM의 Fig.2는 완전한 노이즈 \(\mathbf{x}_T\)로 부터 깨끗한 이미지 \(\mathbf{x}_0\)가 만들어지는 과정을 그리고 있습니다. 즉, \(\mathbf{x}_T, \mathbf{x}_{T-1}, \mathbf{x}_{T-2}, ... , \mathbf{x}_1\)이 어떻게 선택되냐에 따라서 \(\mathbf{x}_0\)가 결정된다는 것이고 DDPM 논문에서 이미지가 생성되는 과정을 이렇게 모델링하는 것입니다. 원인과 결과를 따져보자면 \(\mathbf{x}_0\)는 결과가 되고 \(\mathbf{x}_T, \mathbf{x}_{T-1}, \mathbf{x}_{T-2}, ... , \mathbf{x}_1\)들은 \(\mathbf{x}_0\)라는 결과를 만들어낸 원인이 되는 것입니다.
하지만 오직 \(\mathbf{x}_0\)만 관찰될 수 있고 어떤 \(\mathbf{x}_T\) ~ \(\mathbf{x}_1\)이 선택되어서 지금 보고 있는 \(\mathbf{x}_0\)가 결정되었는지 알 수 없습니다. 이렇게 관찰되는 변수observable variable와 관계되어 영향을 미치지만 직접 관찰되지 않는 변수를 잠재 변수latent variable라 합니다.
앞서 알아본것 처럼 \(\mathbf{x}_0\)의 분포 \(q(\mathbf{x}_0)\)를 알면 이 분포로 부터 \(\mathbf{x}_0\)를 샘플링할 수 있습니다. 찾고 싶은 \(q(\mathbf{x}_0)\)를 신경망 같은 모델로 만들어볼 수 있을 것입니다. 그렇게 신경망 따위로 만든 \(\mathbf{x}_0\)의 분포를 \(p_\theta(\mathbf{x}_0)\)로 쓸 수 있습니다. 이렇게 DDPM에서는 학습으로 만들어가는 분포를 \(p()\)로 적고 원래 있는 분포 다시 말해 찾고 싶은 분포를 \(q()\)로 적습니다. \(p\) 아래 있는 \(\theta\)는 모델이 \(q(\mathbf{x}_0)\)처럼 잘 작동하기 위해 찾아야 하는 파라미터가 됩니다.
\(\mathbf{x}_0, \mathbf{x}_1, ... , \mathbf{x}_T\)들은 서로 연결joint되 있으므로 이 전체 확률변수들의 분포를 \(p_\theta(\mathbf{x}_0, \mathbf{x}_1, ... , \mathbf{x}_T)\) 로 쓸 수 있는데 원문에서는 이를 줄여 \(p_\theta(\mathbf{x}_{0:T})\)로 쓰고 \(\mathbf{x}_{0:T}\)를 \(\mathbf{x}_0, \mathbf{x}_1, ... , \mathbf{x}_T\)들이 모두 결합된 확률변수로 나타냅니다. 최종적으로 관심이 있는 분포는 \(\mathbf{x}_0\)에 대한 분포 이므로 관심 없는 잠재변수는 주변화 시켜 다음처럼 나타낼 수 있습니다.
\[ p_{\theta}(\mathbf{x}_0) = \int p_\theta (\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \]
갑자기 적분 기호가 나와서 머리가 아플 수 있는데 위 식의 의미는 잠재 변수 \(\mathbf{x}_{1:T}\)를 조건으로 \(\mathbf{x}_0\)의 평균을 구한 것으로 생각하면 됩니다. 따라서 \(p_{\theta}(\mathbf{x}_0)\)가 구해진다면 이 분포는 우리에게 잠재 변수를 고려한 평균적인 \(\mathbf{x}_0\)를 샘플링할 수 있게 해줄 것입니다.
만약 \(p_\theta (\mathbf{x}_{0:T})\)를 완전히 알고 있고 이 분포를 사용해서 샘플링하게 된다면 완전 노이즈 이미지 \(\mathbf{x}_T\)와 여러 단계를 거쳐 노이즈가 조금씩 제거된 이미지 \(\mathbf{x}_{T-1}, ... \mathbf{x}_1\), 그리고 마지막 깨끗한 이미지 \(\mathbf{x}_0\)를 모두 한 세트로 뽑을 수 있게 될 것입니다. 그런 샘플링이 가능하다면 다음과 같은 샘플은 뽑힐 가능성이 아주 높을 것입니다.


반면 다음 같이 빨간 캐릭터가 살짝 보이다가 갑자기 하얀 캐릭터로 바뀌면서 노이즈가 제거되는 샘플은 뽑힐 가능성은 아주 낮겠죠.

이렇게 노이즈가 제거 되어 가는 과정에 대한 변수를 한꺼번에 뽑을 수 있는 분포 \(p_\theta (\mathbf{x}_{0:T})\)를 리버스 프로세스reverse process라고 합니다. 이 리버스 프로세스에는 고차원의 확률변수들이 너무 많이 결합되어 있으므로 문제를 간단히 하기 위해 마르코프 가정을 하게 됩니다. 원래는 \(\mathbf{x}_{0}\)에 잠재 변수 \(\mathbf{x}_{1:T}\) 모두가 영향을 미치는 것으로 이야기했지만 모델링 과정에서 마르코프 과정을 가정하고 \(\mathbf{x}_{0}\)에는 \(\mathbf{x}_{1}\)만 잠재 변수가 되게 모델링하게 됩니다. 동일하게 \(\mathbf{x}_{1}\)에는 \(\mathbf{x}_{2}\)만이 잠재 변수가 되겠네요. 마르코프 가정을 하고 각 시간 단계에 대한 이미지의 분포를 다음처럼 정의합니다.
\[ p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t ) := \mathcal{N} \left(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta (\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)\right) \]
위 정의에서 각 이미지에 대한 분포를 정규분포로 가정했습니다. 위 식의 의미는 노이즈가 조금 더 제거된 \(\mathbf{x}_{t-1}\)에 대한 분포는 바로 이전 단계인 노이즈가 약간 더 많은 \(\mathbf{x}_{t}\)를 이용해 계산된 어떤 평균 \(\boldsymbol{\mu}_\theta (\mathbf{x}_t, t)\)와 분산 \(\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)\)을 파라미터로 하는 정규분포로 정의 한다는 것입니다. 이 때 \(\boldsymbol{\mu}_\theta (\mathbf{x}_t, t)\), \(\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)\)같은 것들은 입력 \(\mathbf{x}_t\)를 보고 네트워크가 추정해야 하는 값들 입니다. 다시말해 노이즈가 많은 \(\mathbf{x}_t\)를 네트워크의 입력으로 넣으면 네트워크는 그 입력을 이용해서 정규분포로 가정된 노이즈가 약간 더 적은 \(\mathbf{x}_{t-1}\)의 분포를 평균과 분산을 추정해서 알아내는 것입니다.
마지막 단계인 \(\mathbf{x}_T\)는 순수한 가우시안 노이즈라고 보면 \(p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathbf{I})\)가 되겠고 위 정의와 함께 쓰면 리버스 프로세스 \(p_\theta(\mathbf{x}_{0:T})\)는 마르코프 가정에 의해 다음처럼 모두 곱해진 형태로 정의될 수 있습니다.
\[ p_\theta(\mathbf{x}_{0:T}) := p(\mathbf{x}_T) \prod^{T}_{t=1}p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t) \tag{1} \]
마르코프 가정 덕분에 적어도 무시무시한 적분 기호는 사라졌네요. 😁
포워드 프로세스

멀쩡한 이미지에 노이즈가 점점 확산되어 최종적으로 완전히 노이즈 \(\mathbf{x}_T\)가 되는 과정을 포워드 프로세스forward process라고 합니다. 그림에선 오른쪽에서 왼쪽으로 진행되는 과정입니다. 포워드이라고 하면 보통 왼쪽에 오른쪽으로 진행되는 그림을 상상하게 되는데 논문에서는 유독 이를 거꾸로 그렸습니다. \(\mathbf{x}\)에 대한 인덱스도 0에서 \(T\)까지가 오른쪽에서 왼쪽으로 진행되도록 그려져서 처음 이 그림을 보면 한동안은 포워드 프로세스가 어느 방향인지 계속 햇갈리게 됩니다. 최종 목적이 노이즈로 부터 이미지를 만들어 가는 과정이므로 논문 저자들은 이렇게 반대로 그려놓는 것이 아마 더 자연스럽다고 생각한것 같습니다.
리버스 프로세스를 알아보면서 잠재 변수 \(\mathbf{x}_{1:T}\)는 이미지 \(\mathbf{x}_0\)에 대한 원인이고 \(\mathbf{x}_0\)는 결과라고 했습니다. 결과를 조건으로 하는 원인의 확률을 사후 확률posterior이라고 합니다. 그럼 사후 확률 분포는 \(q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)\)로 쓸 수 있습니다. 이 사후 확률을 포워드 프로세스 또는 디퓨전 프로세스diffusion process라고 합니다. 앞서 이야기한 것처럼 그림에서 오른쪽에서 왼쪽으로 진행되는 과정입니다. 이 확률 분포는 \(\mathbf{x}_0\)가 주어지면 이 이미지를 생성하기 위해 거쳐가야 하는 모든 잠재변수 \(\mathbf{x}_{1:T}\)에 대한 분포를 정의하게 됩니다.
리버스 프로세스는 직접 수식으로 계산할 수 없지만 포워드 프로세스는 마르코프 과정을 상정하고 각 과정이 정규분포라고 가정하면 직접 계산할 수 있습니다. 리버스 프로세스 때와 같이 마르코프 가정을 하면 그림에서 나타낸 노이즈가 조금 적은 \(\mathbf{x}_{t-1}\)을 조건으로 그 다음 노이즈가 조금 더 많은 이미지 \(\mathbf{x}_t\)에 대한 분포는 다음처럼 정의 할 수 있습니다.
\[ q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1} , \beta_t \mathbf{I}) \]
이 식에서 \(\beta_t\)는 각 단계에서 노이즈를 얼마나 추가할 지 결정하게 되는 상수입니다. 이렇게 정의된 개별 분포를 모두 곱해서 잠재 변수에 대한 사후 확률, 포워드 프로세스를 정의 합니다.
\[ q(\mathbf{x}_{1:T} \mid \mathbf{x}_0):= \prod^{T}_{t=1} q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) \tag{2} \]
앞서 리버스 프로세스에서 노이즈를 제거하는 한 단계 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t )\)를 정의한 바 있습니다. 노이즈가 더해지는 과정 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\)로 부터 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\)를 바로 알아 낼 수 있으면 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t )\)를 만들 필요가 없습니다. 하지만 이를 위해 베이즈 정리를 사용한다면 모든 시간 단계에 대한 \(q(\mathbf{x}_t)\)를 다 알아야 하므로 쉽지 않은 일입니다.
\[ q(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \frac{q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)} \]
그래서 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\)의 역과정인 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\)를 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t )\)로 대신하고자 하는게 DDPM에서 하고자 하는 것입니다.
그런데 \(p_\theta(\mathbf{x}_{t-1} \mid \mathbf{x}_t )\)을 잘 만들려면 지도 학습 관점에서 비교 대상인 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\)를 알아야 하는데 이 분포는 모른다고 했으니 학습에 사용할 비교 대상이 없습니다. 이 문제를 인식하고 이를 해결하는 과정을 이해하는 것이 DDPM 논문을 이해하는 거의 전부라 할 수 있으니 차차 알아보도록 하겠습니다.
이제 정의된 포워드 프로세스를 실험해보기 위해 \(\beta_t\), \(T\)같은 값들을 정해야 하는데 DDPM 논문에서는 각 설정값을 다음처럼 지정했다고 나와있습니다.
\(T=1000\), \(\beta_1 = 10^{-4}\), \(\beta_T = 0.02\)
논문과 동일하게 beta() 함수를 작성합니다.
def beta(t, T=1000):
# t: 1~T
# t는 1에서 T까지 이므로 인덱싱할 때는 -1해준다.
return np.linspace(1.0e-4, 0.02, T)[t-1]실험에 사용할 샘플 이미지 \(\mathbf{x}_0\)를 준비합니다. 이때 이미지의 픽셀 값들이 -1, 1사이에 오게 노멀라이즈 합니다.
x0 = (sprites / 255)[10] * 2 - 1
x0.min(), x0.max()(-1.0, 1.0)이 이미지의 크기는 (16,16,3)입니다.
x0.shape(16, 16, 3)분포 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\)를 만들어주는 함수 get_q_xt_given_xtm1()을 정의합니다. 이 함수는 내부에서 \(q(\mathbf{x}_t \mid \mathbf{x}_{t-1})\) 정의에 따라 정규분포를 하나 만들고 그 분포를 반환합니다.
def get_q_xt_given_xtm1(xtm1, t):
beta_t = beta(t)
xtm1_flt = xtm1.reshape(-1)
q = multivariate_normal(
mean=np.sqrt(1-beta_t)*xtm1_flt,
cov=beta_t*np.eye(len(xtm1_flt))
)
return q샘플 x0를 사용해서 \(\mathbf{x}_1\)에 대한 분포를 생성합니다.
# t=1을 지정해 원본 이미지 x0에서 1단계 노이즈 상태인 이미지에 대한 분포를 생성
q_x1_given_x0 = get_q_xt_given_xtm1(x0, t=1)이 분포는 \(\sqrt{1-\beta}\mathbf{x}_0\)를 평균으로 하는 정규분포이므로 \(\mathbf{x}_0\)에 대한 밀도 함숫값, 다시말해 이 분포에서 \(\mathbf{x}_0\)가 존재할 가능성은 크고 일반 노이즈에 대한 가능성은 작아야 합니다. 밀도 함숫값의 로그값을 계산해주는 logpdf() 함수로 확인해봅시다.
# x0에 대한 확률 밀도값 그냥 노이즈에 대한 확률 밀도값
q_x1_given_x0.logpdf( x0.reshape(-1) ), q_x1_given_x0.logpdf( np.random.randn( 16*16*3 ) )(2831.0183943629117, -6699964.090514234)예상대로 \(\mathbf{x}_0\)에 대한 값은 매우 크고 표준 정규분포로 부터 샘플링된 노이즈에 대한 값은 로그값이 매우 작은 음수이므로 거의 0임을 알 수 있습니다. 이제 정의된 분포로부터 \(\mathbf{x}_1\) 하나를 샘플링합니다.
x1 = q_x1_given_x0.rvs(size=1)제대로 작동한다면 x1은 x0와 거의 차이가 없어야 할 것입니다.
fig, ax = plt.subplots(nrows=1, ncols=2)
x0_ = ((x0 - x0.min()) / (x0.max() - x0.min())).clip(0,1)
x1_ = ((x1 - x1.min()) / (x1.max() - x1.min())).clip(0,1)
ax[0].imshow(x1_.reshape(16,16,3))
ax[0].set_title(r"$\mathbf{x}_1$")
ax[1].imshow(x0_.reshape(16,16,3))
ax[1].set_title(r"$\mathbf{x}_0$")
plt.show()
한 스탭정도 노이즈를 확산시켜서는 아무런 차이가 없는듯 보입니다. 경우에 따라 흰색 배경부분을 자세히 보면 완전 흰색이 아니라 약간 색이 달라진 것을 미세하게 확인할 수 있을 수도 있습니다(아주 약하게 나타나거나 모니터에 따라 확인되지 않을 수 있음). 이제 \(T\) 단계까지 한 단계씩 차례로 노이즈를 확산시킵니다. for루프로 이를 직접 구현해보면 다음과 같습니다. 확산 단계는 30단계까지로 제한했습니다.
x0.min(), x0.max()(-1.0, 1.0)%%time
# 루프 돌면서 x30까지 해보기
xts = [x0.reshape(-1).copy()]
xt = xts[0]
T = 30
for t in range(1, T+1):
# t-1 단계에서 만들어진 이미지로 부터 분포 q(x_t|x_t-1)을 만든다.
q_xt_given_xtm1 = get_q_xt_given_xtm1(xt, t)
# 만들어진 분포에서 샘플링한다.
xt = q_xt_given_xtm1.rvs(size=1)
xts.append(xt)CPU times: user 9.76 s, sys: 3.04 s, total: 12.8 s
Wall time: 3.25 s30단계만 진행했는데도 시간이 상당히 오래 걸립니다. 분포를 정의하고 그로 부터 샘플링하는 과정을 기술적으로 잘 처리해서 속도를 조금 높일 수 있겠지만 원리적으로 시간이 오래 걸리는 과정이라는 사실은 변함이 없습니다. 노이즈가 확산된 30개 이미지와 원본이미지를 담은 리스트를 넘파이 어레이로 변환합니다.
xts = np.array(xts)
xts.shape(31, 768)이제 30단계까지 확산된 노이즈를 가진 이미지를 원본 이미지와 비교해보겠습니다.
fig, ax = plt.subplots(nrows=1, ncols=2)
x0_ = ((x0 - x0.min()) / (x0.max() - x0.min())).clip(0,1)
xt_ = ((xt - xt.min()) / (xt.max() - xt.min())).clip(0,1)
ax[0].imshow(xt_.reshape(16,16,3))
ax[0].set_title(f"$\mathbf{{x}}_{{{T}}}$")
ax[1].imshow(x0_.reshape(16,16,3))
ax[1].set_title(r"$\mathbf{x}_0$")
plt.show()
확실이 점점 노이즈로 뒤덮히기 시작합니다. DDPM에서는 \(T=1000\)을 사용하므로 1000단계까지가면 원래 이미지는 완전히 사라지고 노이즈만 있는 이미지가 될 것입니다.
이제 식(2)에 의해 \(q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)\)를 직접 계산할 수 있습니다. \(q(\mathbf{x}_{1:T} \mid \mathbf{x}_0)\)를 직접 눈으로 확인해보기 위해 \(\mathbf{x}_t\)들을 스칼라로 가정하고 \(T=2\)로 두어 \(x_0\), \(x_1\), \(x_2\)로 포워드 프로세스 단계를 제한합니다. 그렇게하면 3차원 그래프로 해당 분포를 그려볼 수 있습니다.
식(2)에 의해 다음과 같으므로
\[ q(x_{1:2} \mid x_0) = q(x_2 \mid x_1) \times q(x_1 \mid x_0) \]
두 일변수 정규분포를 곱하고 정리하면 다음처럼 \(q(x_{1:2} \mid x_0)\)를 \(x_1\), \(x_2\)에 대해 계산해주는 함수를 만들 수 있습니다.
def make_q(x0):
def q(x2, x1):
return (1 / (2*np.pi)) * np.exp( -(1/2) * ((x2-x1)**2 + (x1-x0)**2) )
return q해당 확률분포가 \(x_0\)에 대해서 어떻게 변하는지 확인하기 위해 그림그리는 모듈을 임포트 합니다.
\(x_1\), \(x_2\)는 -10, 10 정도 범위로 설정하고 \(x_0\)는 -5, 5까지 범위를 설정해 각 \(x_0\)에 대해서 \(q(x_{1:2} \mid x_0)\)를 -10, 10로 정의된 정사각 영역에 대해서 함숫값을 모두 계산합니다. 아울러 이렇게 생성된 \(x_0\)에 대해서 \(q(x_{1:2} \mid x_0)\)들이 확률분포로써 타당한지 확인하기 위해 수치적분값이 1이 되는지 확인해봅니다.
from scipy import integrate
# 정의역 정의
x_range = [-10, 10]
y_range = [-10, 10]
x_min, x_max = x_range[0], x_range[1]
y_min, y_max = y_range[0], y_range[1]
xx = np.linspace(x_min, x_max, 150)
yy = np.linspace(y_min, y_max, 150)
X1, X2 = np.meshgrid(xx, yy)
X_grid = np.c_[X1.ravel(), X2.ravel()]
x0s = np.linspace(-5, 5, 21)
Zs = []
for x0_ in x0s:
q = make_q(x0=x0_)
Zs.append( q(X_grid[:,0], X_grid[:,1]) )
# 2차원 수치 적분
print(f"{integrate.dblquad(q, x_range[0], x_range[1], lambda x: y_range[0], lambda x: y_range[1])[0]:.4f}")0.9998
0.9999
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
0.9999
0.9998적분값은 모두 거의 1에 가까운 값임을 확인할 수 있습니다. 이제 앞서 x0s변수에 범위를 잡아둔 \(x_0\)에 따른 \(x_1\), \(x_2\)의 분포를 그림으로 그립니다.
layout = go.Layout(
title='q(x_1:2|x_0)',
width=600, height=600,
margin=dict(l=0, r=0, b=0, t=25),
scene = dict(
xaxis = dict(title='x2', range=[x_min, x_max],),
yaxis = dict(title='x1', range=[y_min, y_max],),
zaxis = dict(title='pdf'),
aspectratio=dict(x=1, y=1, z=0.5)
)
)
# Create figure
fig = go.Figure(layout=layout)
# Add traces, one for each slider step
for Z in Zs:
fig.add_trace(
go.Surface(
x=X_grid[:,0].reshape(X1.shape), y=X_grid[:,1].reshape(X1.shape),
z=Z.reshape(X1.shape),
showscale=False, opacity=1.,
colorscale ='Blues',
contours=dict(
x=dict(show=True, highlight=True),
y=dict(show=True, highlight=True),
z=dict(show=True, highlight=True),
), visible=False
)
)
fig.data[0].visible = True
# Create and add slider
steps = []
for i in range(0, len(fig.data)):
step = dict(
method="update",
args=[
{"visible": [False] * (len(fig.data))},
], # layout attribute
label=f"{x0s[i]:.2f}"
)
step["args"][0]["visible"][i] = True # Toggle i'th trace to "visible"
steps.append(step)
sliders = [
dict(
active=0,
currentvalue={"prefix": "x0: "},
pad={"l":10, "t": 50, "r":10, "b":10},
steps=steps
)
]
fig.update_layout(sliders=sliders)
fig.show()