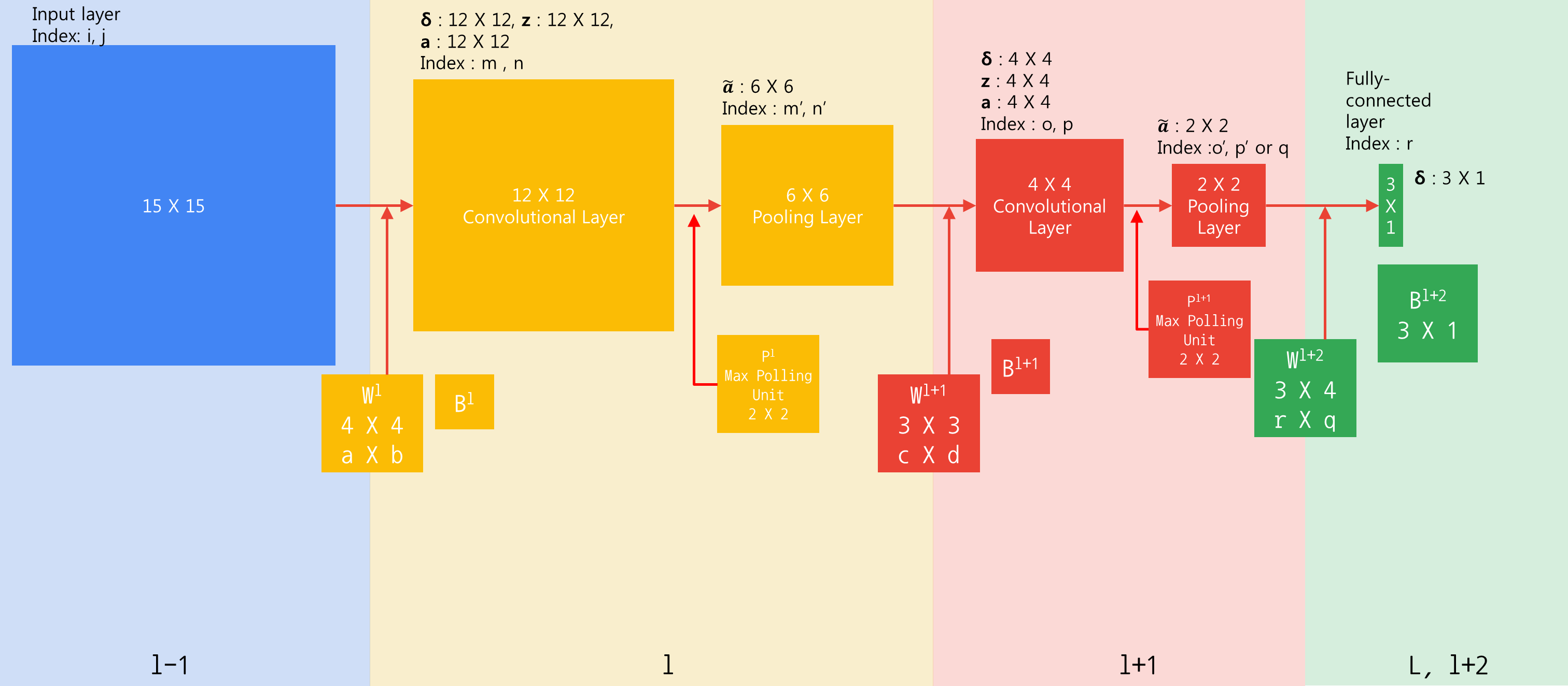
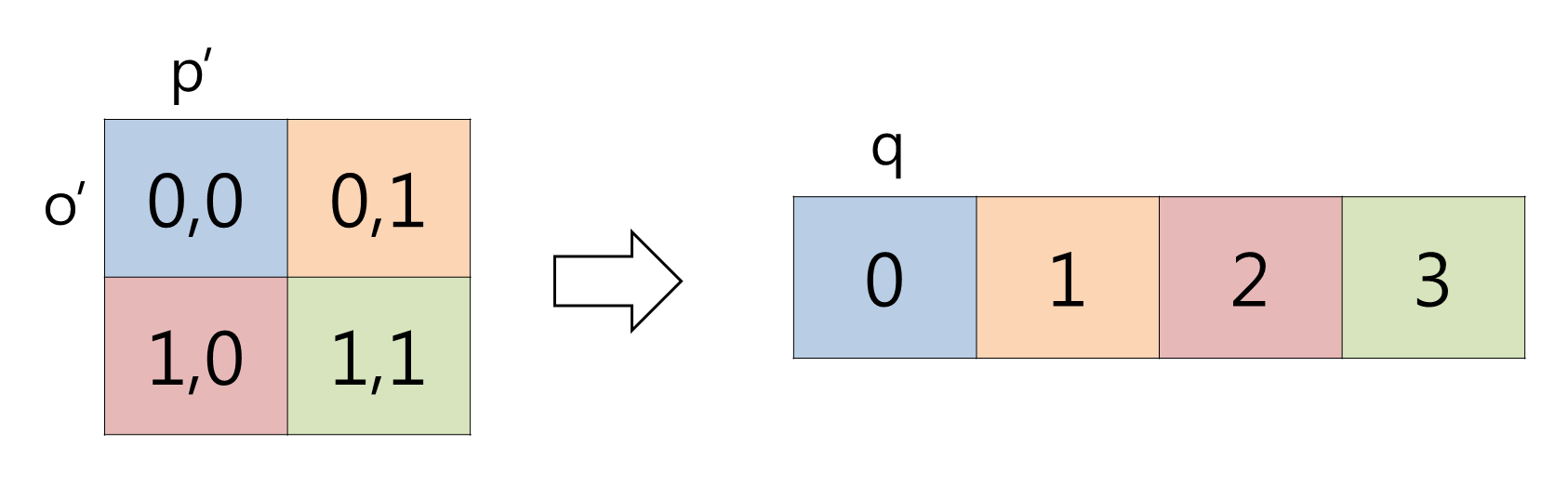
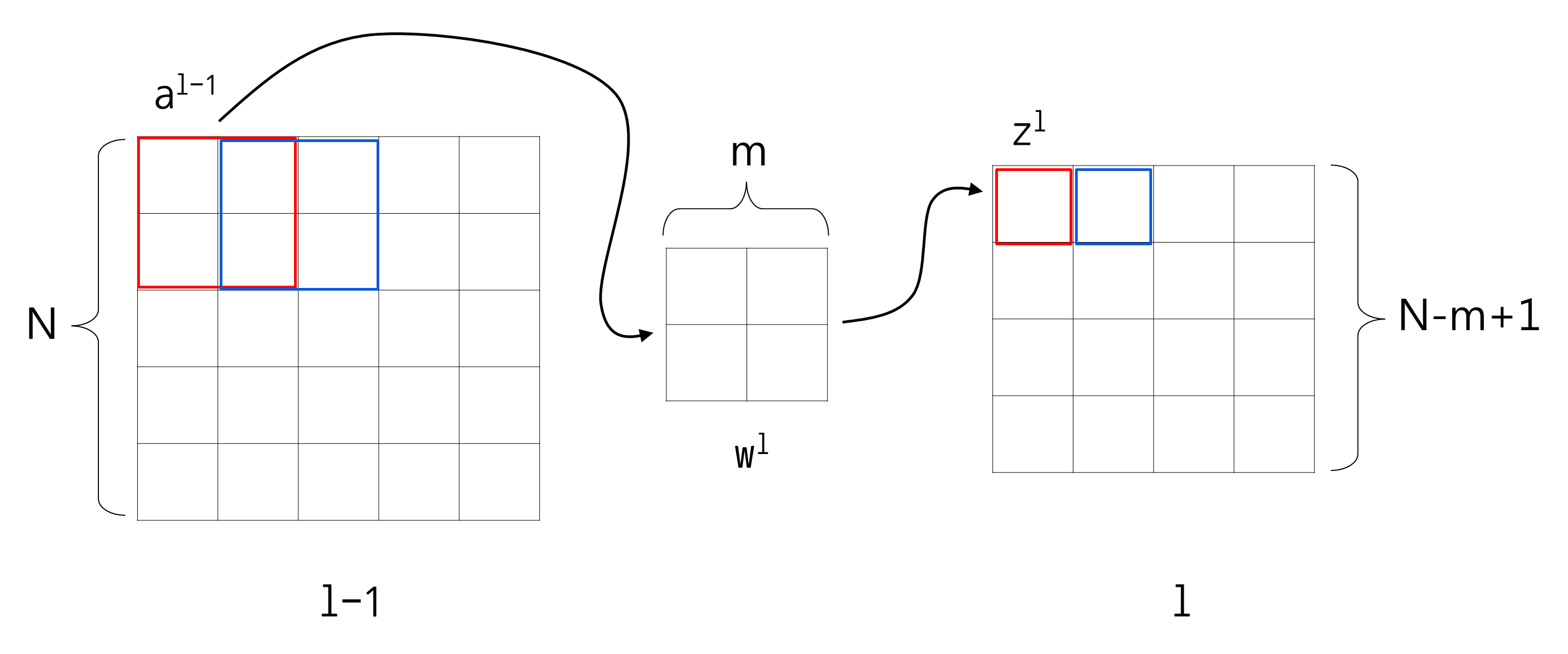
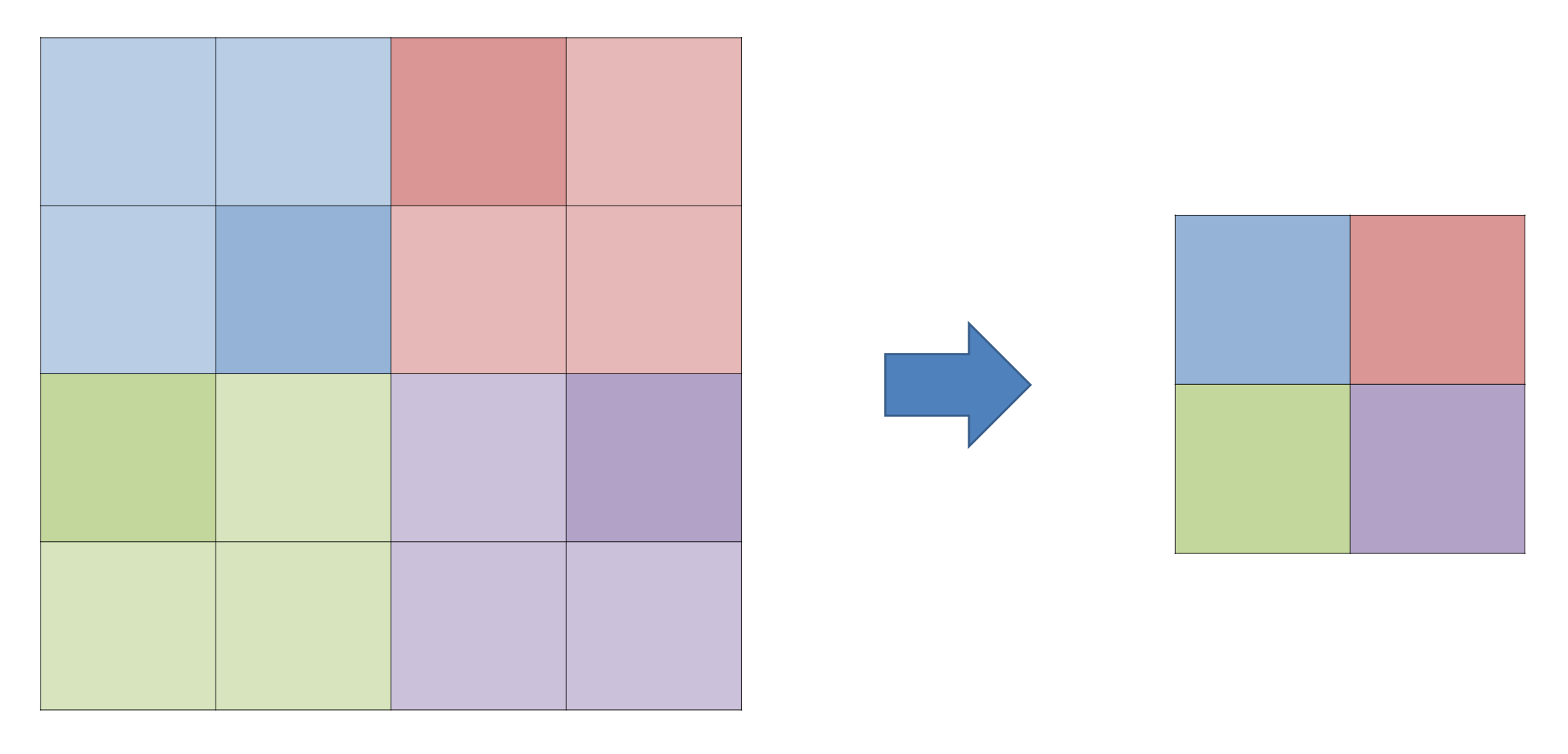
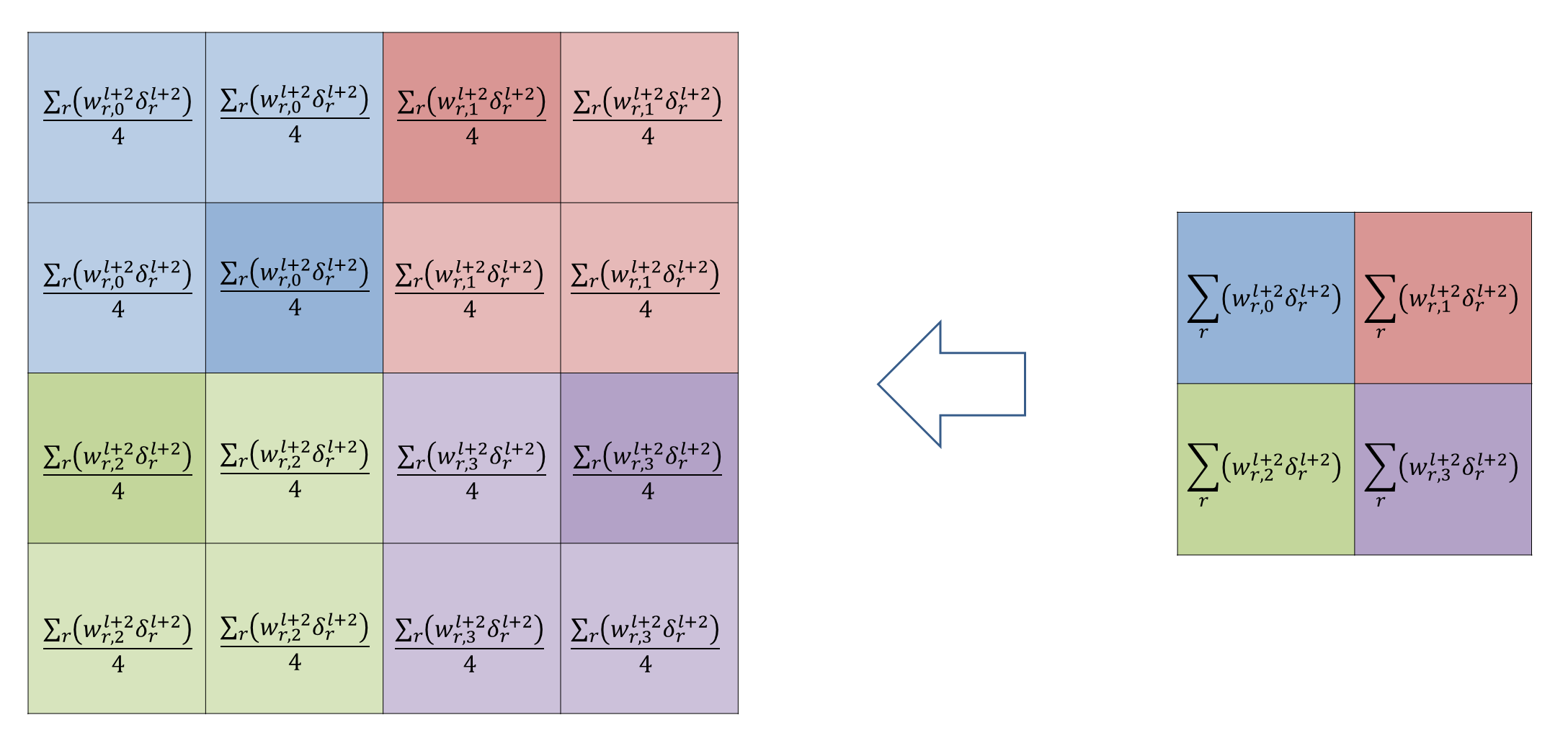
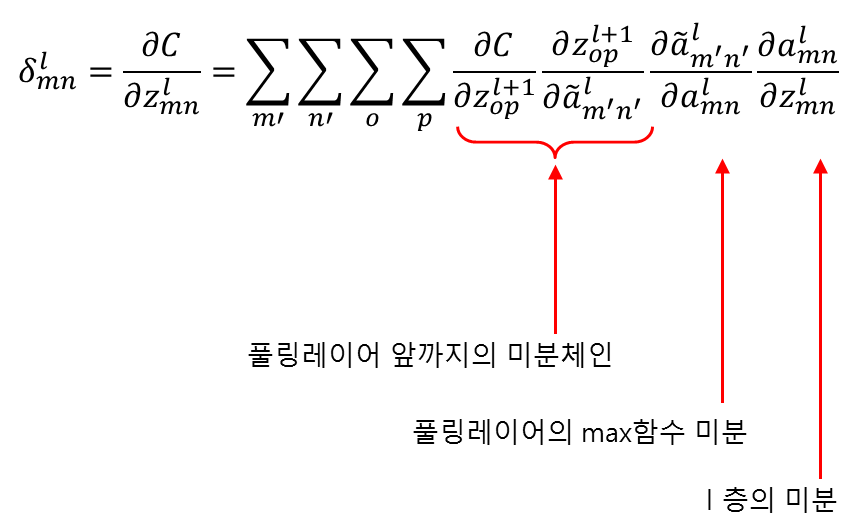
위 식에서
\( z^{l+1}_{op} \)는 식(31)과 같습니다.
$$
z^{l+1}_{op} =
\sum_{c=0}^{C-1} \sum_{d=0}^{D-1}
\left[ w^{l+1}_{cd} \tilde{a}^{l}_{(o+c)(p+d)} \right] + b^{l+1}
$$
식(31)
이제 앞 단계에서와 같은 논리로
\( \frac{\partial z^{l+1}_{op}}{\partial \tilde{a}^{l}_{m' n'}} \)는
식(32)인 경우를 제외하고 모두 0이라는 것을 알 수 있습니다.
$$
m'=o+c \\
n'=p+d
$$
식(32)
식(32)에 의해
\( c=m'-o \),
\( d=n'-p \) 이므로
\( \frac{\partial z^{l+1}_{op}}{\partial \tilde{a}^{l}_{m' n'}} \)은 식(33)과 같습니다.
$$
\frac{\partial z^{l+1}_{op}}{\partial \tilde{a}^{l}_{m' n'}} =
w^{l+1}_{(m'-o)(n'-p)}
$$
식(33)
이제 식(33)의 결과를 이용하여 식(30)을 다시 써보면 식(34)과 같습니다.
$$
\delta^{l}_{mn} =
\frac{\partial C}{\partial z^{l}_{mn} } =
\sum_{m'} \sum_{n'} \sum_{o} \sum_{p}
w^{l+1}_{(m'-o)(n'-p)} \delta^{l+1}_{op}
\frac{\partial \tilde{a}^{l}_{m'n'}}{\partial a^{l}_{mn}}
\frac{\partial a^{l}_{mn}}{\partial z^{l}_{mn}}
$$
식(34)
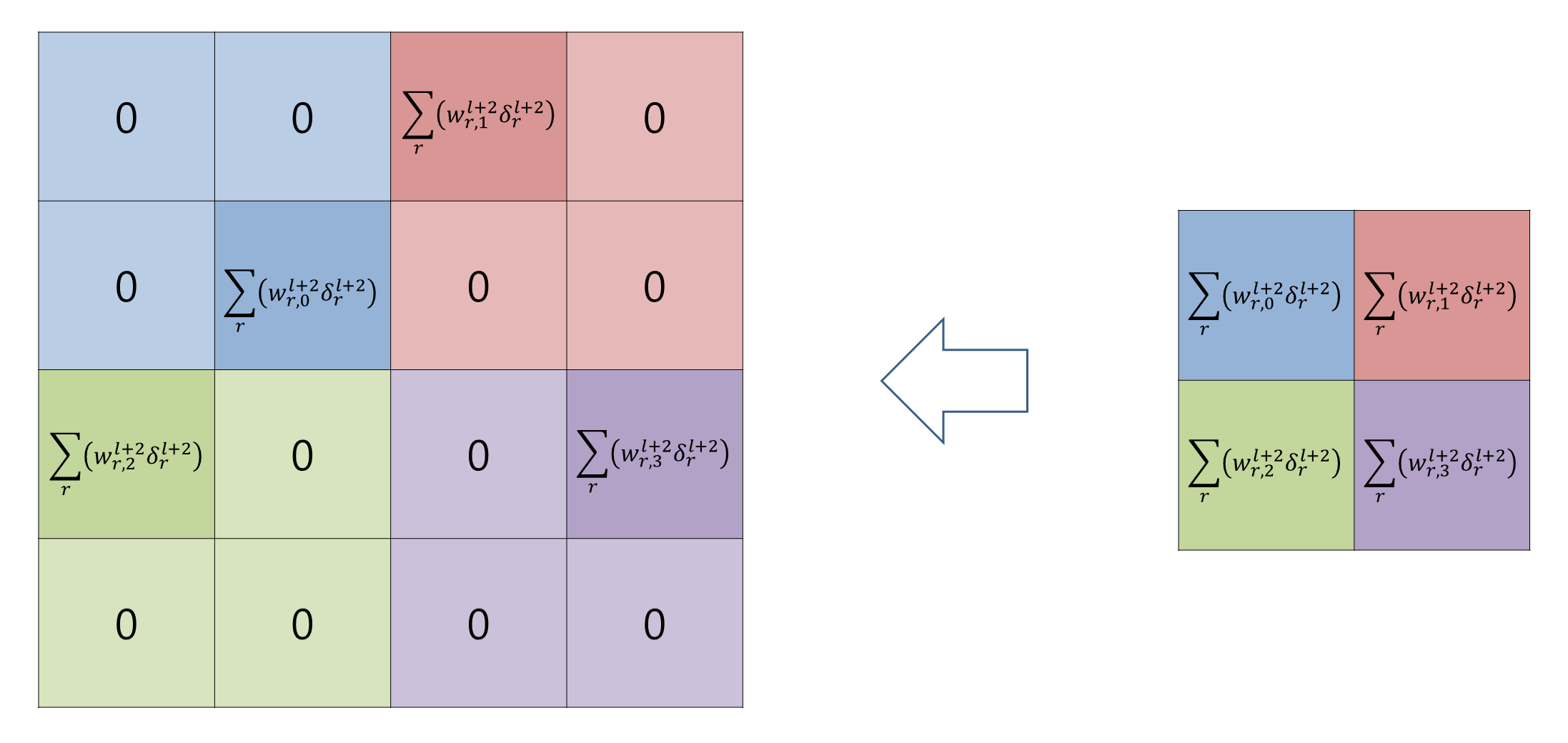
이제 여기서 다시 풀링레이어에 대한 미분
\( \frac{\partial \tilde{a}^{l}_{m'n'}}{\partial a^{l}_{mn}} \)을 처리하도록 하겠습니다.
역시나 이 미분은
\( m'= \lfloor \frac{m}{2} \rfloor \),
\( n'= \lfloor \frac{n}{2} \rfloor \)
인 경우를 제외하고는 모두 0입니다. 따라서 식(34)는 식(35)가 됩니다.
$$
\delta^{l}_{mn} =
\sum_{o} \sum_{p}
w^{l+1}_{(\lfloor m/2 \rfloor -o)(\lfloor n/2 \rfloor -p)} \delta^{l+1}_{op}
\frac{\partial \tilde{a}^{l}_{\lfloor m/2 \rfloor, \lfloor n/2 \rfloor}}{\partial a^{l}_{mn}}
\sigma'(z^{l}_{mn})
$$
식(35)
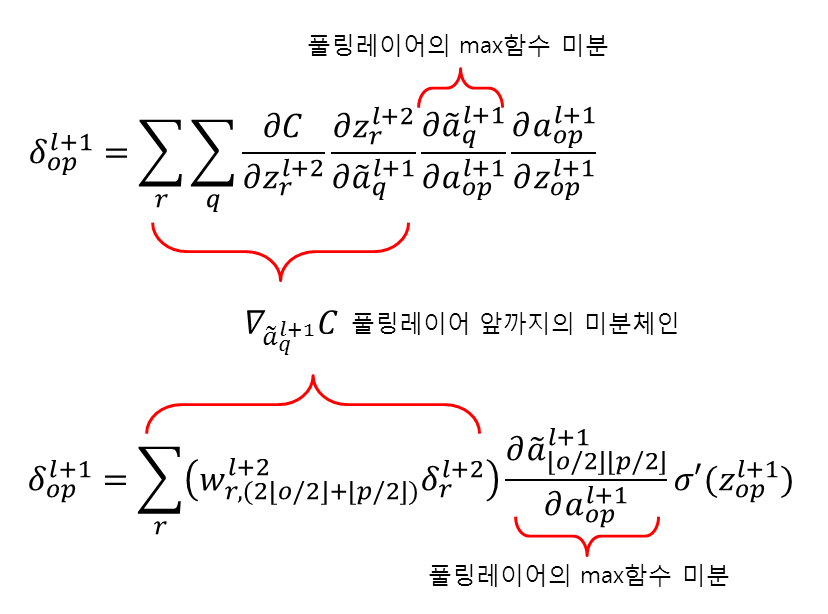
식(35)를 식(21)과 비교해보겠습니다.
$$
\definecolor{black}{RGB}{0,0,0}
\definecolor{spin}{RGB}{251,0,29}
\delta^{l+1}_{op} =
\color{spin}
\sum_{r}
\left( w^{l+2}_{r,(2\lfloor o/2 \rfloor+\lfloor p/2 \rfloor)} \delta^{l+2}_{r} \right)
\color{black}
\frac{\partial \tilde{a}^{l+1}_{\lfloor o/2 \rfloor \lfloor p/2 \rfloor}}{\partial a^{l+1}_{op}} \sigma'(z^{l+1}_{op})
$$
$$
\definecolor{black}{RGB}{0,0,0}
\definecolor{spin}{RGB}{251,0,29}
\delta^{l}_{mn} =
\color{spin}
\sum_{o} \sum_{p} \left(
w^{l+1}_{(\lfloor m/2 \rfloor -o)(\lfloor n/2 \rfloor -p)} \delta^{l+1}_{op}
\right)
\color{black}
\frac{\partial \tilde{a}^{l}_{\lfloor m/2 \rfloor \lfloor n/2 \rfloor}}{\partial a^{l}_{mn}}
\sigma'(z^{l}_{mn})
$$
비교해보면 대부분 같지만
\( w \)와
\( \delta \)사이에서 일어나는 연산이 달라진 것을 확인할 수 있습니다.
\( w \)와
\( \delta \)사이에서 일어나는 연산은 어디에서 많이 본 듯합니다.
앞서 살펴본 식(2)를 다시 보겠습니다.
$$ C(x,y)= \sum_{a=0}^{k-1} \sum_{b=0}^{k-1} I(x-a,y-b)F(a,b) $$
우리가 앞서 살펴본 컨벌루션식인 식(2)와
\( \delta^{l}_{mn} \)을 구할 때
\( w \)와
\( \delta \)사이에서 일어나는 연산이 정확하게
동일하다는 것을 알 수 있습니다.
즉,
\( \mathbf{\delta}^{l+1} \)을 180도 돌려서
\( \mathbf{w}^{l+1} \)에 full 컨벌루션 하는 것입니다.
\( \mathbf{w}^{l+1} \)은 3x3이고 ,
\( \mathbf{\delta}^{l+1} \)은 4x4입니다.
이를 full 컨벌루션 하면 6x6이 되고,
이것이
\( \frac{\partial \tilde{a}^{l}_{\lfloor m/2 \rfloor \lfloor n/2 \rfloor}}{\partial a^{l}_{mn}} \)에 의해
up-sampling되면 12x12가 되어
\( \delta^{l} \)의 차원과 딱 맞게 됩니다.
단계3과 마찬가지로 이제 식(35)을 행렬형태로 써보면 식(36)과 같습니다.
$$
\definecolor{black}{RGB}{0,0,0}
\definecolor{green}{RGB}{45,177,93}
\definecolor{red}{RGB}{251,0,29}
\definecolor{blue}{RGB}{18,110,213}
\mathbf{\delta}^{l} =
\color{red}
\mbox{Upsampling} [
\color{blue}
\mathbf{w}^{l+1} * \mathbf{\delta}^{l+1}
\color{red}
]
\color{black}
\odot
\color{green}
\sigma'(\mathbf{z}^{l})
$$
식(36)
행렬형태로 적으면 간결한 맛은 있지만,
내부적으로 무슨 일이 일어나고 있는지 한눈에 알 기가 힘들어진다는 단점이 있습니다.
그래서 본 글에서는 좀 복잡하지만 인덱스 형태의 식을 고집하였습니다.
단계3의 말미에도 언급하였지만 만약 풀링레이어가 없이 CONV층과 CONV층이 결합된 경우라면 어떻게 될까요?
그럼 식(35)은 식(37)와 같은 간단한 컨벌루션 연산만 남게 됩니다.
$$
\delta^{l}_{mn} =
\sum_{o} \sum_{p}
\left( w^{l+1}_{(m - o)(n - p)} \delta^{l+1}_{op} \right)
\sigma'(z^{l}_{mn})
$$
식(37)
정리하면 식(38)과 같이
\( \delta^{l}_{mn} \)을 구할 수 있습니다.
$$
\definecolor{spin}{RGB}{251,0,29}
\color{spin}
\delta^{l}_{mn} =
\sum_{o} \sum_{p} \left( w^{l+1}_{(\lfloor m/s \rfloor - o)(\lfloor n/s \rfloor - p)} \delta^{l+1}_{op} \right)
\frac{ \partial \tilde{a}^{l}_{\lfloor m/s \rfloor \lfloor n/s \rfloor } }{ \partial a^{l}_{mn} }
\sigma'(z^{l}_{mn})
$$
식(38)
$$
\definecolor{spin}{RGB}{251,0,29}
\color{spin}
\frac{ \partial \tilde{a}^{l}_{\lfloor m/s \rfloor \lfloor n/s \rfloor} }{ \partial a^{l}_{mn} } =
\begin{cases}
1, & \mbox{if } a^{l+1}_{op} = max( nb(a^{l}_{mn}) ) \\
0, & \mbox{ otherwise }
\end{cases}
$$
$$
\definecolor{spin}{RGB}{251,0,29}
\color{spin}
nb(a^{l}_{mn}) \equiv a^{l}_{t \in R_{1} , u \in R_{2}} \\
\color{spin}
\begin{align*}
R_{1} & = [m-(m\%s), \quad m-(m\%s)+(s-1)] \\
\color{spin}
R_{2} & = [n-(n\%s), \quad n-(n\%s)+(s-1)]
\end{align*}
$$
위 식에서,
\( s \)는 풀링레이어 가로 세로 크기
이제 다음 (CBP3), (CBP4)를 이용해
\( \frac{\partial C}{\partial b^{l}} \),
\( \frac{\partial C}{\partial w^{l}_{ab}} \)
을 모두 구할 수 있습니다.
$$
\definecolor{spin}{RGB}{251,0,29}
\begin{align*}
\color{spin}
\frac{\partial C}{\partial b^{l}}
& \color{spin} =
\color{spin}
\sum_{m=0}^{I-A} \sum_{n=0}^{J-B}
\delta^{l}_{mn}
\\
\color{spin}
\frac{\partial C}{\partial w^{l}_{ab}}
& \color{spin} =
\color{spin}
\sum_{m=0}^{I-A} \sum_{n=0}^{J-B}
\tilde{a}^{l-1}_{(m+a)(n+b)} \delta^{l}_{mn}
\end{align*}
$$